Learning mathematics is interesting. It is always lack of understanding the concepts that makes the subject look boring.
One of the common questions asked in Mathematics would be calculating the area of a figure. Area calculations may sound tough to estimate, but if you know the basics and understand the underlying concepts, area calculations turn out to be a walk in a park, be it a triangle, circle, or rectangle.
In the following article, we will try to analyze and grasp the basic concepts of calculating a rectangle area using mathematical and visual clues. At the end, you will be clear on how to calculate the area of a rectangle. Let us learn the basics and then arrive at the calculation part.
Rectangle: What is It?
There are four dots on a piece of paper. When you connect these four dots by four lines, you get a rectangle. A rectangle is described as a figure made of four sides. Like a triangle is one with three sides, a rectangle is nothing but a four-sided figure. In other words, if you connect two dots, you form a line, you join three, and it’s a triangle. Similarly, four dots are connected, and a rectangle is formed.
We find many examples of objects that are rectangular. For instance, the very screen you are looking at while reading this, whether a tablet, desktop, or laptop, is a rectangle. Your study table will also be a rectangle. Similarly, the terrace on the top of a building, the windowpane, the door, the biscuits we eat are generally forms of a rectangle. There are endless examples of rectangles that we come across in our everyday lives. Only if we pay attention, there are mathematical figures everywhere.
Area: What Does it Mean?
An area is nothing but mathematically calculating the space that the figure occupies. . Let us understand it with a simple example. Suppose you can keep a maximum of two small bananas in your mouth without gulping them down. This implies that the area inside your mouth is nothing but space that is occupied by two bananas.
The area is the space that is occupied. When we say that an area inside a building is too small, it simply means that many things cannot be accommodated inside it. Similarly, when we say that the area of the football field is huge, it means a lot of people can be easily accommodated inside the football field. So, whenever there is a mention of the word area, it would simply mean the space occupied.
Area of a Rectangle: How to Calculate It?
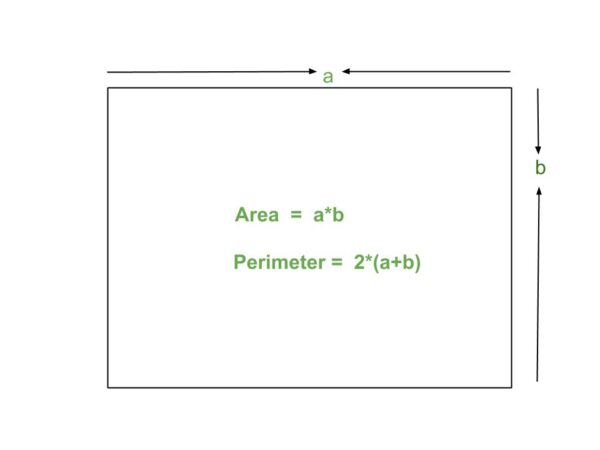
Now that the concept of area is more or less understood, we now move towards the main subject, which is the calculation of the area of a rectangle. To understand this, the two concepts you need to understand are the rectangle’s length and breadth.
A rectangle’s length is nothing but the vertical distance between two points of the rectangle. The breadth is nothing but the horizontal distance between two ends of a rectangle. A simpler way of understanding this is by taking an example of a door inside your home. Let us assume the door of the house is exactly 7 feet tall and 4 feet wide. In this case, the door’s length is 7 feet, and the breadth is 4 feet.
To arrive at the area of a rectangle, we multiply the length with the breadth. In the above example, if we need to calculate the area of the door, we multiply 7 with 4. This turns out to be 28 square feet. This is the door’s area.
In case both the length and width are of the same size, it implies that the figure is a square. For example, if there is a 5 cms wide and 5 cms tall figure, it means it is a square. To calculate the area, we multiply five by five, which is 25 square cms.
Calculating Area of Measurements in Different Formats
In the previous examples,assume that both the dimensions of length and breadth were common. In the above case, it is to be noted that both were measured in feet. Hence, the resultant area calculated would come in square feet. In other words, if we would have taken the measurements in, say, centimetres, the consequent area would be in the format of square centimetres.
In case both the dimensions are in different formats, you need to convert any one of them into the same format. For example, there is a piece of wood with length of 1 meter and a breadth of 4 cm. Thus, you need to convert the same into common dimensions. You can convert the length into 100 cm, and then breadth stays as 4 cm. So, by multiplying 100 by 4, you get 400, and the unit would be square centimetres. One must note that the unit of measurement in the square would be the same as the common dimensional format used.
Here are some more examples of calculating the area of a rectangle:
- Let us assume there is a rectangle of the length of 8 meters and 4 meters wide. The area of the rectangle is thus 32 square meters. To understand the calculation at a deeper level, 32 numbers of uniform squares of 1 meter each would be required to fill the space of the 8 by 4 rectangle. ..
- If there is a rectangle 30 feet in length and 2 feet wide, its area would be 60 square feet. In other words, the space occupied by the figure is equivalent to that of 60 squares of one foot each.
The unit of calculations can also change based on how you want to project your answers. For example, take a rectangle 2-metres in length and 1-metre in breadth. The area comes out to be 2 square metres. If the answer is required in units of square centimetres, then you need to convert both the units into centimetres first.
The above example translates into 200 cms long and 100 cms wide. To calculate the said area, we need to multiply both the figures. Thiscomes to 20,000. Hence, the answer of 2 square meters also translates into a response of 20,000 square centimetres.
Conclusion
To sum up what we have effectively learned, the first step is to arrive at a common dimensional format of length and width of a rectangle. Once that is obtained, the next step is to multiply and arrive at a format which is in square units. This is the final answer to the question of calculating the area of any rectangle.
At the same time, we have also understood what this means by visually comparing the space occupied withsquares of a particular unit. Thus, the next time you come along a sum for the calculation of the area of a rectangle, it should be clear both in your mind and in your answer sheet.
As we had previously stated, learning mathematics is fun when the concepts are visualised and clear. Let your children experience measurement made easy with Cuemath. Their personalised classes by expert teachers will allow your kids to easily learn measurement concepts in an enjoyable and effective manner. Begin enjoying math today!